विशिष्ट आपेक्षिकता/आपेक्षिकता का सिद्धान्त

विशिष्ट आपेक्षिकता

आपेक्षिकता का सिद्धान्त[सम्पादन]

सापेक्षिकता का सिद्धान्त विभिन्न स्थानों पर किये गये प्रेक्षणों के मध्य के सम्बन्ध को निरुपित करता है। यह समस्या पुराने समय से और विभिन्न भौतिक प्रश्नों वाली कठिन सैद्धान्तिक चुनौती रही है। भौतिक प्रश्नों के कुह उदाहरण इस तरह हैं कि हम दो भिन्न वस्तुओं के वेगों को संकलित कैसे करते हैं और चलायमान वस्तुओं के संचरण कैसे एक दूसरे को प्रभावित करते हैं।

इसके लिए सबसे उपयोगी दृष्टिकोणों में से एक है यह कि हम प्रेक्षक के वेग से प्रेक्षणों पर होने वाले प्रभाव का अन्वेषण करें। यह समस्या विभिन्न दार्शनिकों द्वारा समझने का प्रयास किया गया लेकिन यह कार्य गैलीलियो ने किया जो वास्तविक सफलता बना। गैलीलियो (1632) ने अपनी पुस्तक प्रकृति की दो प्रमुख प्रणालियों के बारे में संवाद (मूल शीर्षक: दियालोगो सोपरई दुए मास्सिमी सिस्तेमी देल मोन्दो) में किसी समुद्री जहाज में बैठे लोगों के प्रेक्षणों का उल्लेख किया जो बाहर से प्रेक्षित नहीं हो सकते थे:

"आप जहाज को किसी भी गति से आगे बढ़ा सकते हैं जिसमें आवश्यक है कि गति एकसमान है और इसके रास्ते में उतार-चढ़ाव नहीं हैं। उस स्थिति में आप कोई भी प्रभाव प्रेक्षित करने में असफल रहेंगे और यहाँ तक कि आप यह भी नहीं बता पायेंगे कि जहाज चल रही है अथवा स्थिर है।"

गैलीलियो के अनुसार जब जहाज समरूपता से चलता है तो उसके अन्दर बैठा कोई व्यक्ति यह नहीं ज्ञात कर सकता कि वो गतिशील है। यदि लोग गैलीलियो के गतिशील जहाज में भोजन कर रहे हैं तो उनके हाथ से छूटकर गीरने वाला मटर का उसी तरह सीधा उनकी थाली में नीचे गिरेगा जैसे वो अपने सामान्य शुष्क जगह पर बने घर पर देखते हैं। मटर भी लोगों के साथ गति करते हैं और भोजन करने वाले को विकर्ण (तीरछे) के रूप में गिरते हुये नहीं दिखाई देते। इसका अर्थ यह हुआ कि मटर भी तब तक एकसमान गति में रहेंगे जब तक कोई उनकी गति में बाधा न बने अथवा उनको प्रभावित न करे। इसका अर्थ यह भी है कि यदि जहाज पर लोग कोई भी सामान्य प्रयोग करते हैं तो वह उसी तरह होगा जैसे वह प्रयोग घर पर किया जाता है। यह अवधारणा “गैलीलियो की सापेक्षिकता” कहलाया जिसके अनुसार वस्तुयें अपनी गति को तब तक बनाकर रखती हैं जबतक उन्हें प्रभावित नहीं किया जाये और भौतिकी के नियम प्रयोगशाला की गति पर निर्भर नहीं करते।

इस सामान्य विचार ने अरस्तु के पुराने विचार को चुनौती दे डाली। अरस्तु ने अपनी भौतिकी में तर्क दिया था कि वस्तुयें या तो गति करवायी जाती हैं या फिर विरामावस्था में रहती हैं।^[१] अरस्तु का विचार कुछ जटिल और रुचिकर तर्कों पर आधारित था जिसके अनुसार वस्तुओं को गतिशील बनाये रखने के लिए आवश्यक है कि उन्हें बाहर से गतिशील रखा जाये। इससे अरस्तु ने प्रस्तावित किया कि वस्तुयें एकदम खाली स्थान में भी रुक जायेंगी। यदि अरस्तु का विचार सही होता तो गतिशील जहाज में मटर को आपके निकट गिरना चाहिए था न कि सीधा नीचे थाली में। अरस्तु के विचार को पूर्व में सबने सत्य मान रखा था अतः गैलीलियो का नया विचार असाधारण था और क्योंकि यह भी लगभग सत्य था अतः यह भौतिकी का आधारभूत स्तम्भ बन गया।

गैलीलियो की सापेक्षिकता में दो महत्त्वपूर्ण सिद्धान्त समाहित हैं: पहले के अनुसार यह ज्ञात करना लगभग असम्भव है कि वास्तव में विरामावस्था में कौन है और दूसरे के अनुसार किसी भी वस्तु की एकसमान गति तब तक जारी रहेगी जब तक उसमें कुछ प्रभाव न डाला जाये। दूसरे नियम को गैलीलियो का जड़त्व का नियम अथवा न्यूटन का गति का प्रथम नियम कहा जाता है।

↑ Aristotle (350BC). Physics. http://classics.mit.edu/Aristotle/physics.html

विशिष्ट आपेक्षिकता[सम्पादन]

उन्नीसवीं सदी तक गैलीलियो के सापेक्षिकता सिद्धान्त को सभी प्रेक्षणों में लगाया जाता था चाहे वो कितने भी तेजी से गतिमान हों। यदि आप किसी वस्तु को उत्तरी ध्रुव पर उपर की तरफ फैंकते हैं तो वो सीधे नीचे की तरफ आती है और यह उसी रूप में भूमध्य रेखा पर होता है जबकि ध्रुव की तुलना में भूमध्य रेखा पर पृथ्वी की गति हज़ारों किलोमीटर प्रति घण्टा से तेज गतिमान होती है। गैलीलियो वेगों को सीधा जोड़ दिया जाता था अतः भूमध्य रेखा पर गेंद को उपर की तरफ फैंकने पर भी वह हज़ारों किलोमीटर प्रति घंटा की गति से गतिमान रहती है और जब तक कि इसपर कोई अन्य बाह्य बल आरोपित नहीं किया जाता है, यह गतिमान रहती है।

इस सरल पद्धति पर वर्ष 1865 में तब प्रश्नचिह्न लग गया जब जेम्स क्लेर्क मैक्सवेल ने प्रकाशीय गुणधर्म वाली विद्युत्चुम्बकीय तरंगों के संचरण की व्याख्या के लिए समीकरणों की खोज की। उनकी समीकरणों से स्पष्ट हुआ कि प्रकाश का वेग कुछ नियतांकों पर निर्भर करता है जो भौतिक माध्यम अथवा सर्वव्याप्त “ईथर” माध्यम के साधारण गुणधर्मों पर निर्भर हो सकते हैं। यदि इस स्थिति को माना जाये तो गैलीलियो सापेक्षिकता के अनुसार आपका वेग, आपतित प्रकाश के वेग में जोड़ा जा सकता है। अर्थात् यदि आप प्रकाश के वेग से आधे वेग से गति कर रहे हैं तो ईथर माध्यम में सामने से आपकी तरफ़ आता हुआ प्रकाश का वेग पहले से 1.5 गुणा तेज गति से आता हुआ दिखाई देगा। इसी तरह आपके पीछे की तरफ से आ रहे प्रकाश का वेग आपको ईथर माध्यम में प्रकाश के वेग से आधी गति से आता हुआ प्रतीत होगा। ईथर माध्यम में प्रकाश का वेग हमेशा नियत रहता है अतः यदि आप यदि आप किसी मशाल की रोशनी (प्रकाश) देखते हैं जबकि वो उच्च चाल से गतिमान हो तो प्रकाश की चाल ईथर में बदल जायेगी और यह अपनी सामान्य गति से भिन्न दिखाई देगी। इससे गैलीलियो का सापेक्षिकता सिद्धान्त गलत हो जायेगा क्योंकि आप अलग दिशा में प्रकाश के वेग का मापन करते हुये यह ज्ञात कर सकते हो कि हम स्थिर शुष्क भूमि पर हैं अथवा एक गतिशील जहाज में। चलायमान जहाज में ईथर माध्यम के कारण आपकी गति की दिशा में प्रकाश का वेग कम हो जायेगा और विपरीत दिशा में यह बढ़ जायेगा।

यदि मैक्सवेल समीकरणें वैध हैं और इनका साधारण वेगों का चिरसम्मत योग लागू होता है तो एक ऐसा विशिष्ट निर्देश तंत्र होना चाहिए जो ईथर के साथ स्थिर है। इस विशिष्ट निर्देश तंत्र को वास्तविक शून्य बिन्दु माना जाये जिसके सापेक्ष सभी वेगों का प्रेक्षण करना चाहिए।

विशिष्ट आपेक्षिकता ने भौतिकी में एक सिद्धान्त स्थापित किया जिसमें मैक्सवेल समीकरणें सही हैं और चिरसम्मत वेगों का योग गलत है: कोई विशिष्ट निर्देश तंत्र प्राप्त नहीं किया जा सकता। विशिष्ट आपेक्षिकता ने इसको पुनः स्थापित कर दिया कि सभी जड़त्वीय निर्देश तंत्रों में सभी भौतिक नियम समान रहते हैं और ऐसी कोई घटना प्रेक्षित नहीं की जा सकती जिसमें प्रेक्षक वेगों के निरपेक्ष शून्य को प्राप्त कर सके। आइंस्टीन ने आपेक्षिकता के सिद्धान्त दिये जिनके अनुसार भौतिकी के नियम सभी निर्देश तंत्रों में समान रहते हैं और वो प्रेक्षक के वेग पर निर्भर नहीं करते। आइंस्टीन के अनुसार आप चाहे गैलीलियो के जहाज में हों या लगभग प्रकाश के वेग से गतिशील कार्गो क्षेत्र में, भौतिकी के नियम समान रहेंगे।

आइंस्टीन के विचार भी गैलीलियो के विचारों के अनुरूप थे, दोनों वैज्ञानिकों के अनुसार नियत वेग से गतिशील निर्देश तंत्रों में भौतिकी के सभी नियम गति से अप्रभावी रहेंगे। गैलीलियो से आइंस्टीन तक के समय में वेगों के साधारण योग के साथ भौतिकी के नियमों को समान रखा जाता थ लेकिन आइंस्टीन ने इसमें मैक्सवेल समीकरणों को शामिल करते हुये सरल अवधारणा को अनुकूलित किया।

निर्देश तंत्र, घटनायें और रूपांतरण[सम्पादन]

इस विश्लेषण के साथ आगे बढ़ने से पहले हमें निर्देश तंत्र, घटना और रूपांतरण को अधिक अच्छे से परिभाषित करना चाहिए।

भौतिक प्रेक्षक को 'निर्देश तंत्र के परिवेश के साथ माना जा सकता है, जिसमें कुछ स्थिति और संवेग को निरुपित करने वाले कुछ अक्षों का समाहार होता है अथवा ऐसी अक्ष होती हैं जो भौतिक नियमों को गणितीय रूप में लिखा जा सके।

घटना उसे कहा जाता हैं जो निर्देश तंत्र से पर निर्भर न हो और जिसको चित्रित/वर्णित किया जा सके। रोशनी की चमक अथवा दो वस्तुओं की टक्कर (संघट्ट) एक घटना को निर्मित होंगे।

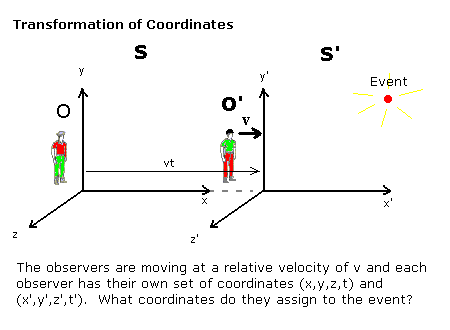
हम एक स्थिति में एक लघु घटना की कल्पना करते हैं जैसे रोशनी की चमक पैदा की जाती है और एक निर्देश तंत्र में प्रेक्षक के लिए उसके निर्देशांक $x,y,z,t$ हैं। उसी घटना को पहले निर्देश तंत्र के सापेक्ष $x$ -अक्ष की दिशा में $v$ वेग से गतिशील निर्देश तंत्र में स्थित प्रेक्षक के लिए क्या निर्देशांक होंगे? इसका सचित्र विवरण निम्नलिखित है:

हम घटना के दूसरे प्रेक्षक के लिए निर्देशांको $x^{'},y^{'},z^{'},t^{'}$ और पहले प्रेक्षक के लिए घटना के निर्देशांको $x,y,z,t$ में सम्बन्ध स्थापित करना चाहते हैं। दोनों प्रेक्षकों के लिए किसी घटना की स्थिति और समय (दिक्-काल) को निर्देशित करने वाले निर्देशांक का मापन करना है, जबकि सरलता के लिए $t=0$ पर दोनों निर्देश तंत्रों को संपाति मान लेते हैं। गैलीलियो सापेक्षिकता के अनुसार:

x^{'}

=x-vt

y^{'}

=

y

z^{'}

=

z

t^{'}

=

t

उपरोक्त समीकरणों के समुच्चय को गैलीलियो निर्देशांक रूपांतरण अथवा गैलीलियो रूपांतरण के रूप में जाना जाता है।

उपरोक्त समीकरणों से एक निर्देश तंत्र में घटना की स्थिति का रूपांतरण दूसरे निर्देश तंत्र में किया जा सकता है। लेकिन क्या होगा जब घटना चलायमान हो? एक निर्देश तंत्र से दूसरे निर्देश तंत्र में वेगों का संयोजन कैसे करते हैं?

वेगों की गणना न्यूटन के सूत्र $v=dx/dt$ से की जाती है। न्यूटनीय भौतिकी का उपयोग वेगों और अन्य भौतिक चरों की गणना में करने के कारण, जब हमें केवल निर्देशांक परिवर्तन से अधिक परिणाम देखने हों तो गैलीलियो के सापेक्षिकता को न्यूटनीय सापेक्षिकता अथवा न्यूटनीय आपेक्षिकता कहते है। वेगों के लिए त्रिविम ज्यामिति में वेग रूपांतरण गैलीलियो सापेक्षिकता के अनुसार:

\mathbf {u_{x}^{'}=u_{x}-v}

\mathbf {u_{y}^{'}=u_{y}}

\mathbf {u_{z}^{'}=u_{z}}

जहाँ $\mathbf {u_{x}^{'},u_{y}^{'},u_{z}^{'}}$ दूसरे प्रेक्षक द्वारा त्रिविम ज्यामिति में गतिशील वस्तु के वेग हैं और $\mathbf {u_{x},u_{y},u_{z}}$ पहले प्रेक्षक द्वारा प्रेक्षित वस्तु के वेग हैं एवं $\mathbf {v}$ प्रेक्षकों का सापेक्ष वेग है। $\mathbf {v}$ में ऋणात्मक चिह्न का अर्थ यह है कि वस्तु दोनों प्रेक्षकों से दूर की तरफ जा रहा है।

यह परिणाम चिरसम्मत वेग संयोजन प्रमेय के रूप में जाना जाता है और दो गैलीलियो निर्देश तंत्रों के मध्य वेगों के रूपांतरण को निरुपित करता है। इसका अर्थ यह है कि प्रेक्षेप्यों के वेग का मान वेग के स्रोत और प्रेक्षेप्यों के लक्ष्य के सापेक्ष ज्ञात किये जाने चाहिए। उदाहरण के लिए जहाज का नाविक कोई पत्थर 10 किमी प्रति घंटा से समुद्र तट पर फैंकता है जबकि जहाज की गति 10 किमी प्रति घंटा है तो पत्थर को समुद्र तट पर 15 किमी प्रति घंटा की गति से टकराना चाहिए।

न्यूटनीय सापेक्षिकता में स्थिति की ज्यामिति को यूक्लिडीन माना जाता है और समय को सभी प्रेक्षकों के लिए समान माना जाता है।

चिरसम्मत वेग संयोजन प्रेमय की व्युत्पत्ति निम्नलिखित है।
गैलीलियो रूपांतरणों को समय के साथ अवकलित करने पर:

$x^{'}=x-vt$

अतः:

$dx^{'}/dt=dx/dt-v$

लेकिन गैलीलियो सापेक्षिकता में, $t^{'}=t$ और अतः $dx^{'}/dt^{'}=dx^{'}/dt$ अतएव:

$dx^{'}/dt^{'}=dx/dt-v$

$dy^{'}/dt^{'}=dy/dt$

$dz^{'}/dt^{'}=dz/dt$

यदि हम $u_{x}^{'}=dx^{'}/dt^{'}$ लिखते हैं तब:

$u_{x}^{'}=u_{x}-v$

$u_{y}^{'}=u_{y}$

$u_{z}^{'}=u_{z}$

विशिष्ट आपेक्षिकता के अभिगृहित[सम्पादन]

पिछले अनुभाग में हमने एक निर्देश तंत्र से दूसरे निर्देश तंत्र में रूपांतरण को देखा जिसमें हमने गैलीलियो के समय में प्रस्तावित साधारण वेगों के योग को काम में लिया। ये रूपांतरण गैलीलियो के मुख्य अभिगृहित के अनुरूप थे जिसके अनुसार सभी जड़त्वीय निर्देश तंत्रों में भौतिकी के नियम समान रहते हैं जिससे कोई यह नहीं बता सकता कि विरामावस्था में कौन है। ईथर की अवधारणा ने गैलीलियो के अभिगृहित में समस्या का अनुमान लगाया क्योंकि ईथर हमेशा विरामावस्था में रहती है और गति की दिशा में प्रकाश के वेग के मापन के साथ प्रेक्षक यह ज्ञात कर सकते हैं कि वो विरामावस्था में हैं या नहीं। आइंस्टीन ने गैलीलियो के मूलभूत अभिगृहित को परिरक्षित रखा कि सभी जड़त्वीय निर्देश तंत्रों में भौतिकी के नियम समान रहते हैं। लेकिन ऐसा करने के लिए उन्होंने एक नया अभिगृहित दिया कि प्रकाश का वेग सभी प्रेक्षकों के लिए समान रहता है। ये अभिगृहित निम्नलिखित रूप में सूचीबद्ध हैं:

1. पहला अभिगृहित: आपेक्षिकता का सिद्धान्त

परिभाषा: सभी जड़त्वीय निर्देश तंत्रों में भौतिकी के नियम समान रहते हैं।

अनौपचारिक: कोई भी भौतिक सिद्धान्त सभी जड़त्वीय प्रेक्षकों को गणितीय रूप में समान दिखाई देना चाहिए। किसी अंतरिक्षयान अथवा सूर्य के चारों ओर चक्कर लगा रहे गृह और गैलेक्सी पर बने भौतिकी के प्रयोगशाला में प्रायोगिक परिणाम समान होंगे, जो प्रयोगशाला की गति पर निर्भर नहीं होंगे।

2. दूसरा अभिगृहित: प्रकाश के वेग की निश्चरता

परिभाषा: मुक्ताकाश में सभी जड़त्वीय निर्देश तंत्रों के लिए प्रकाश का वेग नियत है।

अनौपचारिक: निर्वात में प्रकाश के वेग अथवा चाल को सामान्यतः c से निरुपित किया जाता है, यह सभी जड़त्वीय प्रेक्षकों के लिए, सभी दिशाओं में समान रहता है, और यह प्रकाश उत्सर्जक वस्तु के वेग पर निर्भर नहीं करता।

इन अभिगृहितों की सहायता से आइंस्टीन ने यह प्रदर्शित किया कि घटानाओं के प्रेक्षण पर प्रेक्षक के वेग से कैसे प्रभावित होती हैं। इसकी सहायता से वो एक भौतिक-सिद्धान्त देने में सफल हुये जो द्रव्यमान और ऊर्जा में तुल्यता का पूर्वानुमान लगाने और शुरूआती क्वांटम सिद्धान्तों को समझाने में सफल रहा।

आइंस्टीन के आपेक्षिकता के नियमों को आपेक्षिकता का विद्युत्गतिकी दृष्टिकोण के रूप में जाना है। ज्यादातर उन्नत पाठ्यपुस्तकों में इसे दिक्-काल दृष्टिकोण के रूप में उल्लिखिति किया गया है, जिनमें भौतिकी के नियम अपने आप में दिक्-काल में सममिति के कारण हैं और दिक्-काल के अस्तित्व का प्राकृतिक परिणाम ही प्रकाश की चाल की नियतता है। हालांकि आइंस्टीन का दृष्टिकोण में बल और इसके प्रभाव को समान रूप से वैध माना गया था जो आधुनिक भौतिकी में और अधिक अलग तरिके से समझा जाता है।

आइंस्टीन का आपेक्षिकता सिद्धान्त - विद्युत्गतिकी दृष्टिकोण[सम्पादन]

आइंस्टीन ने यह समझने का प्रयास किया जब दो भिन्न-भिन्न प्रेक्षक प्रकाश की चाल को नियत प्रेक्षित करते हैं तो लम्बाई और समय में परिवर्तन को कैसे समझा जा सकता है। उन्होंने दोनों प्रेक्षकों के लिए प्रकाश के वेग के सूत्र को देखा जो $(x=ct)$ और $(x^{'}=ct^{'})$ होने चाहिए, जब प्रेक्षकों की आपेक्षिक गति से $x^{'}$ अक्ष लगातार आगे बढ़ रही है उस स्थिति में प्रकाश की चाल के प्रेक्षण को समान मान रखने के लिए क्या नियतांक प्रस्तावित करना चाहिए। उनके कार्य को विस्तार से परिशिष्ट में दिखाया गया है। इस गणना का परिणाम लोरेन्ट्स रूपांतरण समीकरणें हैं:

x'=\gamma (x-vt)\,

y'=y\,

z'=z\,

t'=\gamma (t-{\frac {vx}{c^{2}}})\,

यहाँ पर नियतांक $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ है। ये समीकरणें किन्हीं भी आपेक्षिक गति वाले दो प्रेक्षकों पर लागू होती हैं लेकिन कोष्टक में स्थित चिह्न वेग की दिशा के अनुसार बदल जाता है - अधिक जानकारे के लिए परिशिष्ट देखें।

लोरेन्ट्स रूपांतरण, अतिरिक्त अभिधारणाओं के साथ गैलीलियो रूपांतरण के तुल्य हैं, यह अतिरिक्त अभिधारणा यह है कि प्रकाश की चाल सभी के लिए समान रहेगी चाहे वो कितने भी तेजी से यात्रा कर रहे हों। प्रकाश की चाल दूरी और समय का अनुपात है (जिसका मात्रक मीटर प्रति सैकण्ड है) अतः सभी को प्रकाश की चाल का समान मान का मापन हो इसके लिए आवश्यक है कि मापक छड़ों, प्रकाश स्रोतों और के मध्य एवं अभिग्राही के मध्य की दिक्काश दूरी और घड़ी की टिक-टिक की संख्या प्रेक्षकों के मध्य गतिकीय भिन्नता रखने चाहिए। अतः आपेक्षिक वेग (v) वाले दो प्रेक्षकों के साथ लम्बाई और समयान्तरालों में परिवर्तन को लोरेन्ट्स रूपान्तरण से उल्लिखित किया जा सकता है। सभी प्रेक्षक प्रकाश की चाल की गणना प्रकाश की कीरण द्वारा तय की दूरी और उसमें लगे समय के अनुपात से ज्ञात कर सकते हैं तथा सबको प्रकाश की चाल का मान समान ही प्राप्त होगा।

आइंस्टीन का दृष्टिकोण "विद्युत्गतिकी" वाला रहा क्योंकि उसमें मैक्सवैल समीकरणों को आधार माना गया था जिनके अनुसार प्रकाश एक नियत वेग से चलता है। जैसा कि उपर वर्णित है, सार्वत्रिक नियत वेग का विचार बहुत ही विचित्र था क्योंकि वेग को विस्थापन (सरल शब्दों में दूरी) और समय के अनुपात के रूप में समझा जाता है। क्या लोरेन्ट्स रूपांतरण समीकरणों में दिक् और काल (समय) के बारे में गूढ़ सत्य छुपा हुआ है? आइंस्टीन ने इसका सबसे स्पष्ट वर्णन प्रस्तुत किया जिसके अनुसार लोरेन्ट्स रूपांतरण समीकरणें वास्तव में दिक् और काल के गुणधर्मों को उल्लिखित करती हैं।^[१] उनका सामान्य तर्क नीचे दिया गया है।

यदि समीकरणों को संयुग्मित किया जाता है तो वो निम्नलिखित सम्बंध को संतुष्ट करती हैं:

(1) $x^{'2}-c^{2}t^{'2}=x^{2}-c^{2}t^{2}\,$

आइंस्टीन (1920) ने दिक्काश में किसी भी दिशा में संवेग को वर्णित करने के लिए भी इसको चित्रित किया:

(2) $x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,$

समीकरण (2) ब्रह्माण्ड में लम्बाइयों एवं समयों के मध्य सम्बंधों के बारे में ज्यामितीय अभिगृहित है। इसके अनुसार नियतांक s इस प्रकार होता है कि:

s^{2}=x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}\,

s^{2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,

इस समीकरण को मिन्कोवस्की द्वारा पायथोगोरस प्रमेय (जो कि $s^{2}=x^{2}+y^{2}$ ) है) के विस्तृत रूप के रूप में पहचाना गया, बीसवीं सदी के पूर्वार्द्ध में ऐसे विस्तार सामान्य रूप में जाने जाते थे। इस तरह लोरेन्ट्स समीकरणों से यह समझा जा सकता है कि ब्रह्माण्ड चतुर्विमीय दिक्-काल से बना हुआ है और इसके परिणामस्वरूप किसी भी "ईथर" माध्यम की आवश्यकता नहीं है। (आइंस्टीन 1920 देखें^[१], लोरेन्ट्स रूपांतरण से आइंस्टीन ने कैसे चतुर्विमीय ब्रह्माण्ड को वर्णित किया यह परिशिष्टों में दिखाया गया है जिसमें "दूरीक प्रदिश" के उपयोग के रूप में "काल्पनिक समय" को प्रतिस्थापित किया जाता है।)

आइंस्टीन के विश्लेषण के अनुसार दो प्रेक्षकों की आपेक्षिकीय गति में x-अक्ष और समय अक्ष एक दूसरे को नहीं काटती। एक प्रेक्षक का समय से दूसरे प्रेक्षक के समय को सम्बंधित करने वाली समीकरण में देखा जा सकता है कि x-अक्ष के अनुदिश दूरी इस सम्बंध को परिवर्तित करती है:

t'=\gamma (t-{\frac {vx}{c^{2}}})\,

इसका अर्थ यह हुआ कि "निर्देश तंत्र" के पूर्ण विचार को ही पुनः समझने की आवश्यकता है जिसमें अक्षें एक दूसरे को नहीं काटती।

↑ ^१.० ^१.१ Einstein, A. (1920). Relativity. The Special and General Theory. Methuen & Co Ltd 1920. Written December, 1916. Robert W. Lawson (आधिकारिक अनुवाद). http://www.bartleby.com/173/

जड़त्वीय निर्देश तंत्र[सम्पादन]

समय के लिए लोरेन्ट्स रूपांतरण में $(vx/c^{2})$ का घटक शामिल है जो x-अक्ष के सापेक्ष गतिशील प्रेक्षक गतिशील प्रेक्षक के लिए भिन्न परिणाम देता है। इसका अर्थ यह हुआ कि वो पुराने निर्देश तंत्र अब लागू नहीं होंगे जिसमें दिक् (ज्यामितिय) विमायें ही काम में ली जाती थी और समय सभी निर्देश तंत्रों में समान रहता था। भिन्न-भिन्न प्रेक्षकों के लिए "निर्देश तंत्र" की तुलनात्मक अवधारणाओं में प्रेक्षक की घड़ी को शामिल करके विस्तृत किया जाना आवश्यक है।

एक "जड़त्वीय निर्देश तंत्र" कुछ छड़ों को समकोण रखते हुये जोड़कर बनायी गई काल्पनिक, त्रिविमीय संरचना से निरुपित कर सकते हैं जिसमें प्रत्येक बिन्दु को पारस्परिक तुल्यकालिक घड़ियों के साथ जोड़ दिया जाता है (जैसा निम्नलिखित चित्र में दर्शाया गया है)। कोई वस्तु किसी जड़त्वीय निर्देश का भाग अथवा उससे जुड़ी हुई कहलायेगी यदि यह वस्तु घड़ियों की तुल्याकालिकता नहीं बदलती और निर्देश तंत्र में नियत ज्यामितिय स्थिति रखती है। जड़त्वीय निर्देश तंत्र जो जिसमें गतिशील वस्तु जो घूर्णन की स्थिति में नहीं है (अघूर्णी), को उस वस्तु के लिए जड़त्वीय विराम निर्देशतंत्र कहते हैं। एक जड़त्वीय निर्देशतंत्र किसी विशिष्ट वस्तु के लिए विराम निर्देश तंत्र होता है लेकिन वह वस्तु पारस्परिक रूप से गतिमान प्रेक्षक को निर्देशतंत्र के साथ गतिशील दिखाई देगी।

इस तरह के निर्देश तंत्र "जड़त्वीय" निर्देश तंत्र कहलाते हैं। हम आगे इसी पुस्तक में इसका अध्ययन करेंगे कि न्यूटन के गति के प्रथम नियम जिसे जड़त्व का नियम कहते हैं, के अनुसार परस्पर गतिमान वस्तुओं (जहाँ घूर्णन, गुरुत्वीय बल अथवा बाह्य बलों का अभाव हो) के लिए एक उभयनिष्ट विराम निर्देशतंत्र प्राप्त कर सकते हैं जिसमें घड़ियाँ (समय) तुल्यकालिकता में भिन्नता रखता है और समान छड़ की लम्बाई परस्पर गतिमान और विराम निर्देशतंत्रों में भिन्न प्रेक्षित होगी।

इसी तरह से "जड़त्वीय निर्देश तंत्र" की विभिन्न अन्य परिभाषायें भी यहाँ पर दी जा सकती हैं लेकिन इनमें से अधिकतर निर्देशांकों के निरूपण और/अथवा व्यवस्था के आवश्यक विवरण उपलब्ध करवाने में अक्षम होती हैं और मूलभूत परिभाषा से व्युत्पन्न होती हैं। इन परिभाषाओं का एक उदाहरण इस प्रकार है: "एक जड़त्वीय निर्देशतंत्र ऐसा निर्देश तंत्र है जिसमें न्यूटन का गति का प्रथम नियम वैध रहता है।"

ब्लैंडफोर्ड और थोर्न (2004) द्वारा दी गयी निम्नलिखित परिभाषा^[१] काम करने वाले भौतिक विज्ञानियों के लिए जड़त्वीय निर्देशतंत्र के अर्थ को पूर्णतः स्पष्ट करने का सारांश है::

"एक जड़त्वीय निर्देशतंत्र छड़ों और समय के मापन के लिए काम में ली जाने वाली (काल्पनिक) त्रि-विमीय संरचना है जो निम्नलिखित गुणधर्मों का पालन करे: (क) संरचना दिक्-काल में मुक्त रूप से गतिमान हो (अर्थात् इसपर कोई बल कार्य नहीं कर रहा हो) और घूर्णदर्शी से जुड़ा हुआ हो जिससे यह दूरस्त, भौतिक वस्तुओं के साथ घूर्णन न करे। (ख) लाम्बिक संरचना में जुड़ी प्रेक्षण छड़ें हों जिनपर तुलना करने पर एकसमान रेखाखण्डों अंकित हों, उदाहरण के लिए किसी मानक प्रकार के परमाणु अथवा अणु से उत्सर्जित प्रकाश का तरंगदैर्घ्य; अतः छड़ें प्रसामान्य कार्तिय निर्देशतंत्र को निरूपित करेंगी जिनमें एक का प्रेक्षण x-अक्ष के मापन को निरूपित करेगा, दूसरी का मापन y-अक्ष और तीसरी का मापन z-अक्ष को निरूपित करेगा। (ग) समय-घड़ियों को इस संरचना में सघन रूप से जोड़ा गया है जिससे संरचना के सभी बिन्दुओं पर एक अलग समय-घड़ी उपलब्ध हो। (घ) घड़ियों की टिक की आवाज की जब तुलना की जाती है तो यह समरूप प्राप्त हो, उदाहरण के लिए किसी मानक प्रकार के परमाणु अथवा अणु द्वारा उत्सर्जित प्रकाश का समय, ये आदर्श घड़ियाँ होती हैं। (च) घड़ियाँ आइंस्टीन तुल्यकालन प्रक्रिया से तुल्यकालिक होनी चाहिए: यदि प्रकाश का एक कम्पन एक घड़ी द्वारा उत्सर्जित किया जाता है तो यह दूसरी घडी के दर्पण से टकराकर वापस आना चाहिए और इस टक्कर में लगे समय $t_{b}$ टक्कर में भेजने वाली घड़ी और उत्सर्जक घड़ी में लगय समयों का औसत होना चाहिए: $t_{b}=1/2(t_{e}+t_{r})$ .¹
¹आदर्श घड़ियों की प्रकृति के गहराई से अध्ययन के लिए और छड़ों के आदर्श मापन के लिए माइनर, थोर्न और व्हीलर (1973) की पुस्तक में पृष्ठ संख्या 23 से 29 और 395 से 399 देखें।"

विशिष्ट आपेक्षिकता, वस्तुओं के जड़त्वीय विराम निर्देश तंत्रों के सापेक्ष एक दूसरे से भिन्न गतिशील निर्देशतंत्रों में गति को प्रदर्शित करती है। प्रत्येक प्रेक्षक एक दूसरे प्रेक्षक को गतिशील ही देखता है तो जड़त्वीय निर्देशतंत्र विकृत प्रतीत होता है। यह खोज विशिष्ट आपेक्षिकता का मूलतत्व है जिसका अर्थ यह है कि गतिशील निर्देशतंत्रों के मध्य निर्देशांकों का रूपांतरण कठिन है। इसकी आगे गहराई से चर्चा की जायेगी।

↑ Blandford, R.D. and Thorne, K.S.(2004). Applications of Classical Physics. California Institute of Technology. See: http://www.pma.caltech.edu/Courses/ph136/yr2004/

[Aristotle-1] Aristotle (350BC). Physics. http://classics.mit.edu/Aristotle/physics.html

[Einstein1920-2] १.० ^१.१ Einstein, A. (1920). Relativity. The Special and General Theory. Methuen & Co Ltd 1920. Written December, 1916. Robert W. Lawson (आधिकारिक अनुवाद). http://www.bartleby.com/173/

[BT2004-3] Blandford, R.D. and Thorne, K.S.(2004). Applications of Classical Physics. California Institute of Technology. See: http://www.pma.caltech.edu/Courses/ph136/yr2004/

[१]

[१]

[१]